Diffusion Model的理论基础

references:

• Understanding Diffusion Models: A Unified Perspective https://arxiv.org/abs/2208.11970

• Denoising Diffusion Probabilistic Models https://arxiv.org/abs/2006.11239

近年来，Diffusion Model在图像/视频生成领域以及VLA模型都表现出优异性能，本文参考上述文献，试图以简单扼要的篇幅解释清楚Diffusion Model的数学原理，适合有CS和Machine Learning背景的读者快速入门。

Introduction

生成模型领域有几个well-known的方向，包括 Generative Adversarial Networks (GANs)，likelihood-based，energy-based以及score-based，Variational Diffusion Models (VDM) 的数学原理可以从多个方向进行解释，本文选择likelihood-based，个人认为比较好理解。

likelihood-based的方法的核心思想是：给定一个数据集$X_D$，训练模型来最大化数据集中样本（evidence）的出现概率（likelihood），进而拟合到$P_{\phi}(x)$，即数据的真实分布。这类方法中最具代表性的就是Variational Autoencoders (VAEs)，而VDM可以认为VAE的一个变体，因此本文从VAE讲起，逐步递进至VDM。

VAE

likelihood-based生成模型的核心目标是拟合出数据的真实分布（$P_{\phi}(x) \rightarrow P(x)$)，但只有数据分布还不够，因为数据生成过程本质是在真实的数据分布中采样，对于一个完全未知的复杂分布是很难采样的，因此，VAE借助一个随机变量$z$和自定义分布$P(z)$（一般选择多维的标准高斯分布$N~(z; 0,I)$ ），并通过$q(z|x)$（Encoder）和$p(x|z)$（Decoder）将$z$和$x$建立起联系。这样，对符合高斯分布的$z$采样，就能通过Decoder得到一个新的生成数据$x’$，$z$被叫做隐变量（latent variable）。

所谓Variational Autoencoders，Autoencoder是指通过编解码的过程，将数据压缩至低维空间；Variational是指对隐空间（latent space）施加约束，迫使它成为正态分布，进而为整个数据空间提供了生成能力。

然而直接最大化likelihood是困难的，最大化某个复杂变量常用的方法是最大化它的某个下界。由引理1可以把likelihood $logP(x)$ 拆成两项，即$E_{q_{\phi}(z|x)} [log \frac {p(x,z)} {q_{\phi}(z|x)}]$和$D_{KL}[q_{\phi}(z|x)||p(z|x)]$，KL散度的定义决定了它是大于等于0的，所以第一项就是likelihood的一个下界，称做Evidence Lower Bound (ELBO)。

进一步分析最大化ELBO是在做什么，由lemma 1得 $logP(x) = E_{q_{\phi}(z|x)} [log \frac {p(x,z)} {q_{\phi}(z|x)}] + D_{KL}[q_{\phi}(z|x)||p(z|x)]$，等号左边和参数$\Phi$没关系（可以视作关于$\Phi$ 定值），因此通过调整参数$\Phi$来最大化ELBO，实际上就是在最小化$q_{\phi}(z|x)$Encoder和真实的后验概率$p(z|x)$之间的KL散度，这正是我们想要的。完美！

这里你可能想问，最大化ELBO就是在优化encoder了，那decoder在哪里优化呢？答案就是在ELBO里面了，接下来继续分析ELBO。

由lemma 2可知，$ELBO = E_{q_{\phi}(z|x)} [log {p_{\theta}(x|z)}] - D_{KL}(q_{\phi}(z|x)||p(z))$，最大化ELBO就是要最大化第一项并最小化第二项。拆开来看，第一项是在Decoder从隐变量z生成原始数据x的概率，被称为reconstruction term，用于优化Decoder；第二项是由Encoder映射到的隐变量z分布和指定的分布$p(z)$之间的KL散度，被称作prior matching term，用于优化Encoder。

这里结合一下VAE模型的实际实现，进一步理解上述的两个优化项在工程中是如何实现的。在实际的VAE的模型中，Encoder拟合的变分分布通常被假设为一个对角高斯（各维度独立的正态分布），即$q_{\phi}(z|x) = N(z;\mu_{\phi}(x),\delta^2_{\phi}(x))$，而prior分布$p(z)$通常选取标准的多元高斯$N(z; 0, I)$。对于prior matching term，KL散度是可以直接计算的；对于reconstruction term，期望的计算则往往利用蒙特卡洛估计进行近似，即

$$\arg\max_{\phi, \theta} \mathbb{E}_{q_{\phi}(z|x)} \left[ \log p_{\theta}(x|z) \right] - D_{KL}(q_{\phi}(z|x) \parallel p(z)) \approx \arg\max_{\phi, \theta} \sum_{l=1}^{L} \log p_{\theta}(x|z^{(l)}) - D_{KL}(q_{\phi}(z|x) \parallel p(z))$$

而直接采样的操作是不可导的，需要用重参数化技巧，非本文重点不多展开。

MHVAE （Markovian Hierarchical Variational Autoencoders）

MHVAE是一种特殊的VAE，它引入了T个隐变量$z_{1:T}$，将编/解码的过程分成T步，也就是所谓的级联Hierarchical。同时，每一步的编/解码只和它的上一步状态有关，和更早的状态无关，即马尔可夫性质Markovian。

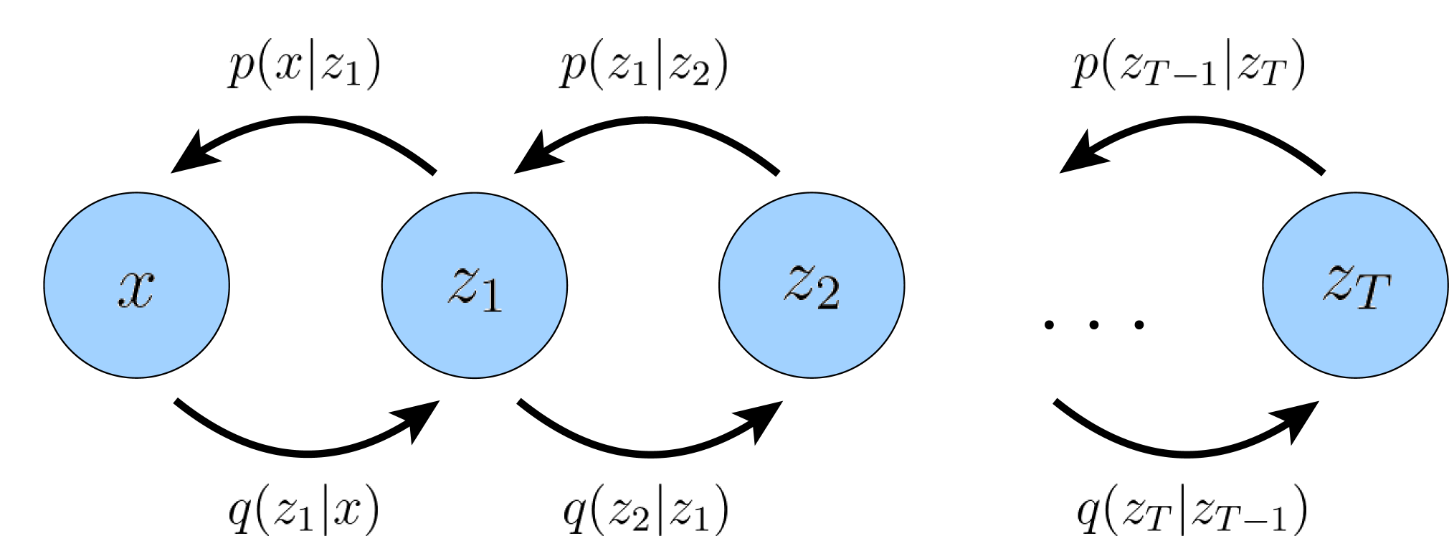
由lemma 1易得，$logp(x) \ge \mathbb{E}_{q_{\phi}(z_{1:T}|x)} \left[ \log \frac{p(x, z_{1:T})}{q_{\phi}(z_{1:T}|x)} \right]$。

VDM (Variational Diffusion Model)

VDM是MHVAE在以下三个限制条件的特例：

1. 数据$x$和所有隐变量$z_t$的维度相同；
2. 所有的encoder $q(zt|z{t-1})$都是预定义好的高斯分布模型（不需要学习），即$zt$状态为以$z{t-1}$为均值的高斯分布；
3. 最终T状态的分布$z_T$为标准高斯分布。

这里做一下符号变换 $x\rightarrow x_0, z_t->x_t$，限制1和2指定了$q(x_t|x_{t-1}) \sim N(x_t, \sqrt\alpha_tx_{t-1}, (1-\alpha_t)I)$, $\alpha_t$是VDM中的超参，一般认为指定，有些后续方法也将其设定为可学习。限制3指定$p(x_T) \sim N(0,I)$。

既然VDM是VAE的变体，那思路不变，最大化Evidence的过程依然是去最大化ELBO，接下来就讲一下如何获得VDM的ELBO。

由lemma 3可得，$ELBO = \underbrace{\mathbb{E}_{q(x_1|x_0)}[\log p_{\theta}(x_0|x_1)]}_{\text{reconstruction term}} - \underbrace{\mathbb{E}_{q(x_{T-1}|x_0)}[D_{KL}(q(x_T|x_{T-1}) \parallel p(x_T))]}_{\text{prior matching term}} - \sum_{t=1}^{T-1} \underbrace{\mathbb{E}_{q(x_{t-1}, x_{t+1}|x_0)}[D_{KL}(q(x_t|x_{t-1}) \parallel p_{\theta}(x_t|x_{t+1}))]}_{\text{consistency term}}$，接下来看一下这三项的物理含义。

1. 第一项被称作reconstruction term，表示的是基于第一步的隐变量原始数据分布的log probability；
2. 第二项被称作prior matching term，表示最后一步的encode分布和最终隐变量的分布之间的KL散度，其中没有可优化的参数，由于我们假设在T足够大时$p(x_T)$也是高斯，这一项可以视作0；
3. 第三项被称作consistency term，表示对于某个中间隐状态，denoising step from a noisier image should match the corresponding noising step from a cleaner image。

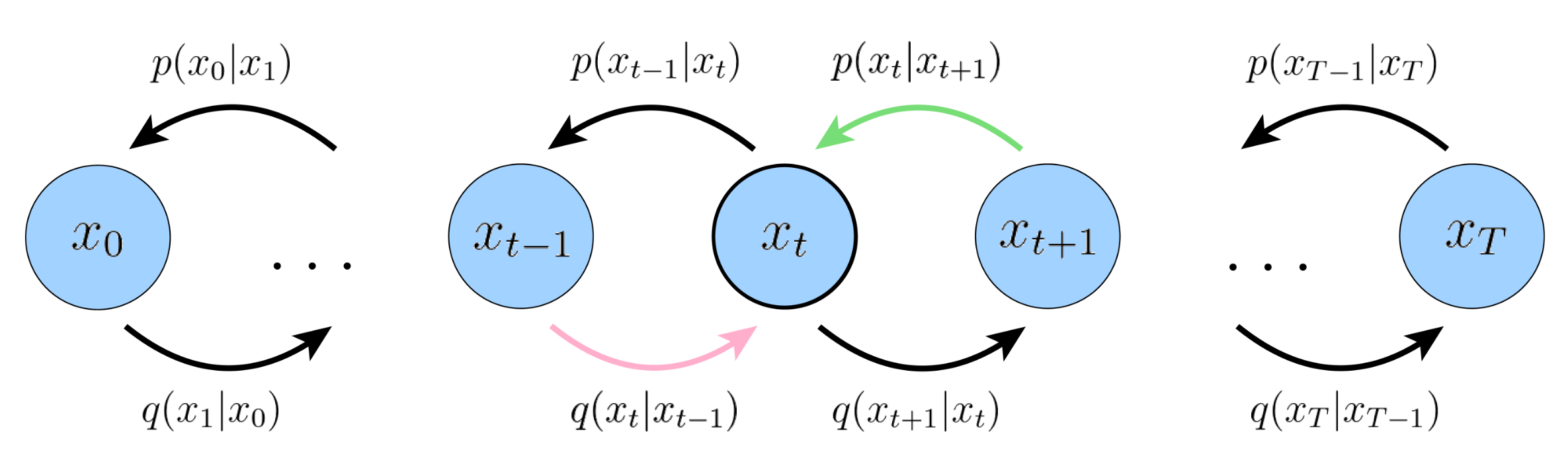
目前ELBO中的三项都是期望，需要通过蒙特卡洛方法进行估计，然而对于consistency term，它依据的两个随机变量（$x_{t-1}$和$x_{t+1}$）的期望，这会使得方差变大，估计值更加不准，因此需要进一步推导。

利用马尔可夫性质和贝叶斯公式，可得$q(x_t|x_{t-1}) = q(x_t|x_{t-1}, x_0) = \frac{q(x_{t-1}|x_t, x_0)q(x_t|x_0)}{q(x_{t-1}|x_0)}$，将这个关键步骤带入ELBO得推导过程（具体过程见lemma 4），可得$ELBO = \underbrace{\mathbb{E}_{q(x_1|x_0)}[\log p_{\theta}(x_0|x_1)]}_{\text{reconstruction error}} - \underbrace{D_{KL}(q(x_T|x_0) \parallel p(x_T))}_{\text{prior matching term}} - \sum_{t=2}^{T} \underbrace{\mathbb{E}_{q(x_t|x_0)}[D_{KL}(q(x_{t-1}|x_t, x_0) \parallel p_{\theta}(x_{t-1}|x_t))]}_{\text{transition matching terms}}$ 。第一项和VAE类似不再赘述，第二项没有可优化参数可以忽略，重点关注第三项，$q(x_{t-1}|x_t,x_0)$是未知分布，直接拟合是比较困难的，需要对其进行进一步推导。

由于$q(xt|x{t-1})$是预定义好的高斯分布，容易想到用贝叶斯公式对$q(x_{t-1}|x_t, x_0)$进项转化，$q(x_{t-1}|x_t,x_0) = \frac{q(x_t|x_{t-1},x_0)q(x_{t-1}|x_0)}{q(x_t|x_0)}$，但其中还带了 $q(x_{t-1}|x_0)$和$q(x_t|x_0)$，由lemma 5得，它们也是高斯分布，$x_t \sim N(x_t; \sqrt{\overline\alpha_t} x_0, (1-\overline\alpha_t)I$，其中$\overline\alpha_t=\prod_{i=0}^t{\alpha_t}$。带入推导过程，可以得到$q(x_{t-1}|x_t,x_0)$也是一个高斯分布（具体过程见lemma 6），$x_{t-1} \sim N(x_{t-1}; \frac{\sqrt{\alpha_t}(1-\bar{\alpha}_{t-1})x_t + \sqrt{\bar{\alpha}_{t-1}}(1-\alpha_t)x_0}{1-\bar{\alpha}_t}, \frac{(1-\alpha_t)(1-\bar{\alpha}_{t-1})}{1-\bar{\alpha}_t}\mathbf{I})$ 。我们假设$p_\theta(x_{t-1}|x_t)$也是高斯分布，由于$x_t$以及$\alpha_t,\bar{\alpha_t}$在这个分布中都是给定的，为了方便对应，可以将$p_\theta(x_{t-1}|x_t)$的形式设置为$N(x_{t-1}; \frac{\sqrt{\alpha_t}(1-\bar{\alpha}_{t-1})x_t + \sqrt{\bar{\alpha}_{t-1}}(1-\alpha_t)\hat{x_{\theta}}(x_t,t)}{1-\bar{\alpha}_t}, \frac{(1-\alpha_t)(1-\bar{\alpha}_{t-1})}{1-\bar{\alpha}_t}\mathbf{I})$，那么两个高斯分布直接之间KL散度$D_{KL}(q(x_{t-1}|x_t, x_0) \parallel p_{\theta}(x_{t-1}|x_t))$就可以转化为$x_\theta(x_t,t)$和$x_0$之间的差距了，由lemma 7可得，

$$D_{KL}(q(x_{t-1}|x_t, x_0) \parallel p_{\theta}(x_{t-1}|x_t)) = \frac{1}{2} \left( \frac{\bar{\alpha}_{t-1}}{1 - \bar{\alpha}_{t-1}} - \frac{\bar{\alpha}_t}{1 - \bar{\alpha}_t} \right) \left[ \| \hat{x}_{\theta}(x_t, t) - x_0 \|_2^2 \right]$$

到目前为止，优化目标已经被转为训练一个映射$\hat x_\theta$，它基于步数t和第t步得隐变量$x_t$，恢复出$x_0$，这已经是一个可训练的目标了。另外，还可以利用$x_0 = \frac{x_t-\sqrt{1-\overline\alpha_t}\epsilon_0}{\sqrt{\overline\alpha_t}}$，将优化目标转化为预测第t步加在$x_0$上的噪声（具体过程见lemma 8）。实践结论表明，预测噪声效果会更好，DDPM就是使用这种方式。

Lemmas

lemma1: 拆分likelihood获得ELBO

$$\begin{align*} \log p(x) &= \log p(x) \int q_\phi(z|x) dz \\ &= \int q_\phi(z|x) (\log p(x)) dz \\ &= \mathbb{E}_{q_\phi(z|x)} [\log p(x)] \\ &= \mathbb{E}_{q_\phi(z|x)} \left[ \log \frac{p(x, z)}{p(z|x)} \right] \\ &= \mathbb{E}_{q_\phi(z|x)} \left[ \log \frac{p(x, z) q_\phi(z|x)}{p(z|x) q_\phi(z|x)} \right] \\ &= \mathbb{E}_{q_\phi(z|x)} \left[ \log \frac{p(x, z)}{q_\phi(z|x)} \right] + \mathbb{E}_{q_\phi(z|x)} \left[ \log \frac{q_\phi(z|x)}{p(z|x)} \right] \\ &= \mathbb{E}_{q_\phi(z|x)} \left[ \log \frac{p(x, z)}{q_\phi(z|x)} \right] + D_{KL}(q_\phi(z|x) \parallel p(z|x)) \\ &\geq \mathbb{E}_{q_\phi(z|x)} \left[ \log \frac{p(x, z)}{q_\phi(z|x)} \right] \end{align*}$$

lemma2: ELBO分解

$$\begin{align*} \mathbb{E}_{q_\phi(z|x)} \left[ \log \frac{p(x, z)}{q_\phi(z|x)} \right] &= \mathbb{E}_{q_\phi(z|x)} \left[ \log \frac{p_\theta(x|z) p(z)}{q_\phi(z|x)} \right] \\ &= \mathbb{E}_{q_\phi(z|x)} [\log p_\theta(x|z)] + \mathbb{E}_{q_\phi(z|x)} \left[ \log \frac{p(z)}{q_\phi(z|x)} \right] \\ &= \underbrace{\mathbb{E}_{q_\phi(z|x)} [\log p_\theta(x|z)]}_{\text{reconstruction term}} - \underbrace{D_{KL}(q_\phi(z|x) \parallel p(z))}_{\text{prior matching term}} \end{align*}$$

lemma3: VDM ELBO推导1

$$\begin{align*} \log p(x) &= \log \int p(x_{0:T}) q(x_{1:T}|x_0) dx_{1:T} \\ &= \log \int \frac{p(x_{0:T}) q(x_{1:T}|x_0)}{q(x_{1:T}|x_0)} dx_{1:T} \\ &= \log \mathbb{E}_{q(x_{1:T}|x_0)} \left[ \frac{p(x_{0:T})}{q(x_{1:T}|x_0)} \right] \\ &\geq \mathbb{E}_{q(x_{1:T}|x_0)} \left[ \log \frac{p(x_{0:T})}{q(x_{1:T}|x_0)} \right] \\ &= \mathbb{E}_{q(x_{1:T}|x_0)} \left[ \log \frac{p(x_T) \prod_{t=1}^T p_\theta(x_{t-1}|x_t)}{\prod_{t=1}^T q(x_t|x_{t-1})} \right] \\ &= \mathbb{E}_{q(x_{1:T}|x_0)} \left[ \log \frac{p(x_T) p_\theta(x_0|x_1) \prod_{t=2}^T p_\theta(x_{t-1}|x_t)}{q(x_T|x_{T-1}) \prod_{t=1}^{T-1} q(x_t|x_{t-1})} \right] \\ &= \mathbb{E}_{q(x_{1:T}|x_0)} \left[ \log \frac{p(x_T) p_\theta(x_0|x_1) \prod_{t=1}^{T-1} p_\theta(x_t|x_{t+1})}{q(x_T|x_{T-1}) \prod_{t=1}^{T-1} q(x_t|x_{t-1})} \right] \\ &= \mathbb{E}_{q(x_{1:T}|x_0)} \left[ \log \frac{p(x_T) p_\theta(x_0|x_1)}{q(x_T|x_{T-1})} \right] + \mathbb{E}_{q(x_{1:T}|x_0)} \left[ \log \prod_{t=1}^{T-1} \frac{p_\theta(x_t|x_{t+1})}{q(x_t|x_{t-1})} \right] \\ &= \mathbb{E}_{q(x_{1:T}|x_0)} [\log p_\theta(x_0|x_1)] + \underbrace{\mathbb{E}_{q(x_{T-1}, x_T|x_0)} \left[ \log \frac{p(x_T)}{q(x_T|x_{T-1})} \right]}_{\text{prior matching term}} + \sum_{t=1}^{T-1} \mathbb{E}_{q(x_{1:t}, x_{t+1}|x_0)} \left[ \log \frac{p_\theta(x_t|x_{t+1})}{q(x_t|x_{t-1})} \right] \\ &= \underbrace{\mathbb{E}_{q(x_1|x_0)} [\log p_\theta(x_0|x_1)]}_{\text{reconstruction term}} + \underbrace{\mathbb{E}_{q(x_{T-1}, x_T|x_0)} \left[ D_{KL}(q(x_T|x_{T-1}) \parallel p(x_T)) \right]}_{\text{prior matching term}} \\ &\quad - \sum_{t=1}^{T-1} \underbrace{\mathbb{E}_{q(x_{t-1}, x_{t+1}|x_0)} \left[ D_{KL}(q(x_t|x_{t-1}) \parallel p_\theta(x_t|x_{t+1})) \right]}_{\text{consistency term}} \end{align*}$$

1. VDM ELBO推导2

$$\begin{align*} \log p(x) &\geq \mathbb{E}_{q(x_{1:T} | x_0)} \left[ \log \frac{p(x_{0:T})}{q(x_{1:T} | x_0)} \right] \\ &= \mathbb{E}_{q(x_{1:T} | x_0)} \left[ \log \frac{p(x_T) \prod_{t=1}^T p_\theta(x_{t-1} | x_t)}{\prod_{t=1}^T q(x_t | x_{t-1})} \right] \\ &= \mathbb{E}_{q(x_{1:T} | x_0)} \left[ \log \frac{p(x_T) p_\theta(x_0 | x_1) \prod_{t=2}^T p_\theta(x_{t-1} | x_t)}{q(x_1 | x_0) \prod_{t=2}^T q(x_t | x_{t-1})} \right] \\ &= \mathbb{E}_{q(x_{1:T} | x_0)} \left[ \log \frac{p(x_T) p_\theta(x_0 | x_1) \prod_{t=2}^T p_\theta(x_{t-1} | x_t)}{q(x_1 | x_0) \prod_{t=2}^T q(x_t | x_{t-1}, x_0)} \right] \\ &= \mathbb{E}_{q(x_{1:T} | x_0)} \left[ \log \frac{p_\theta(x_T) p_\theta(x_0 | x_1)}{q(x_1 | x_0)} + \log \prod_{t=2}^T \frac{p_\theta(x_{t-1} | x_t)}{\frac{q(x_{t-1} | x_t, x_0) q(x_t | x_0)}{q(x_{t-1} | x_0)}} \right] \\ &= \mathbb{E}_{q(x_{1:T}|x_0)} \left[ \log \frac{p(x_T) p_\theta(x_0|x_1)}{q(x_1|x_0)} + \log \prod_{t=2}^T \frac{p_\theta(x_{t-1}|x_t)}{\frac{q(x_{t-1}|x_t, x_0) q(x_t|x_0)}{q(x_{t-1}|x_0)}} \right] \\ &= \mathbb{E}_{q(x_{1:T}|x_0)} \left[ \log \frac{p(x_T) p_\theta(x_0|x_1)}{q(x_1|x_0)} + \log \frac{q(x_1|x_0)}{q(x_T|x_0)} + \log \prod_{t=2}^T \frac{p_\theta(x_{t-1}|x_t)}{q(x_{t-1}|x_t, x_0)} \right] \\ &= \mathbb{E}_{q(x_{1:T}|x_0)} \left[ \log \frac{p(x_T) p_\theta(x_0|x_1)}{q(x_T|x_0)} + \sum_{t=2}^T \log \frac{p_\theta(x_{t-1}|x_t)}{q(x_{t-1}|x_t, x_0)} \right] \\ &= \mathbb{E}_{q(x_{1:T}|x_0)} \left[ \log p_\theta(x_0|x_1) \right] + \mathbb{E}_{q(x_T|x_0)} \left[ \log \frac{p(x_T)}{q(x_T|x_0)} \right] + \sum_{t=2}^T \mathbb{E}_{q(x_{t}, x_{t-1}|x_0)} \left[ \log \frac{p_\theta(x_{t-1}|x_t)}{q(x_{t-1}|x_t, x_0)} \right] \\ &= \underbrace{\mathbb{E}_{q(x_1|x_0)} \left[ \log p_\theta(x_0|x_1) \right]}_{\text{reconstruction term}} - \underbrace{D_{KL}(q(x_T|x_0) \parallel p(x_T))}_{\text{prior matching term}} - \sum_{t=2}^T \underbrace{\mathbb{E}_{q(x_t|x_0)} \left[ D_{KL}(q(x_{t-1}|x_t, x_0) \parallel p_\theta(x_{t-1}|x_t)) \right]}_{\text{denoising matching term}} \end{align*}$$

lemma 5: $p(x_t|x_0)$得推导过程

$$\begin{align*} x_t &= \sqrt{\alpha_t} x_{t-1} + \sqrt{1 - \alpha_t} \epsilon^*_{t-1} \\ &= \sqrt{\alpha_t} \left( \sqrt{\alpha_{t-1}} x_{t-2} + \sqrt{1 - \alpha_{t-1}} \epsilon^*_{t-2} \right) + \sqrt{1 - \alpha_t} \epsilon^*_{t-1} \\ &= \sqrt{\alpha_t \alpha_{t-1}} x_{t-2} + \sqrt{\alpha_t - \alpha_t \alpha_{t-1}} \epsilon^*_{t-2} + \sqrt{1 - \alpha_t} \epsilon^*_{t-1} \\ &= \sqrt{\alpha_t \alpha_{t-1}} x_{t-2} + \sqrt{\alpha_t - \alpha_t \alpha_{t-1}} \epsilon^*_{t-2} + \sqrt{1 - \alpha_t} \epsilon^*_{t-1} \\ &= \sqrt{\alpha_t \alpha_{t-1}} x_{t-2} + \sqrt{\alpha_t - \alpha_t \alpha_{t-1} + 1 - \alpha_t} \epsilon_{t-2} \\ &= \sqrt{\alpha_t \alpha_{t-1}} x_{t-2} + \sqrt{1 - \alpha_t \alpha_{t-1}} \epsilon_{t-2} \\ &= \ldots \\ &= \sqrt{\prod_{i=1}^{t} \alpha_i} x_0 + \sqrt{1 - \prod_{i=1}^{t} \alpha_i} \epsilon_0 \\ &= \sqrt{\bar{\alpha}_t} x_0 + \sqrt{1 - \bar{\alpha}_t} \epsilon_0 \\ &\sim \mathcal{N}(x_t; \sqrt{\bar{\alpha}_t} x_0, (1 - \bar{\alpha}_t) \mathbf{I}) \end{align*}$$

lemma 6: $p(x{t-1}|x{t},x_0)$推导过程

$$\begin{align*} q(x_{t-1}|x_t, x_0) &= \frac{q(x_t|x_{t-1}, x_0) q(x_{t-1}|x_0)}{q(x_t|x_0)} \\ &= \frac{\mathcal{N}(x_t; \sqrt{\alpha_t} x_{t-1}, (1 - \alpha_t) \mathbf{I}) \mathcal{N}(x_{t-1}; \sqrt{\alpha_{t-1}} x_0, (1 - \alpha_{t-1}) \mathbf{I})}{\mathcal{N}(x_t; \sqrt{\alpha_t} x_0, (1 - \alpha_t) \mathbf{I})} \\ &\propto \exp \left\{ -\frac{1}{2(1 - \alpha_t)} \left[ (x_t - \sqrt{\alpha_t} x_{t-1})^2 + (x_{t-1} - \sqrt{\alpha_{t-1}} x_0)^2 - (x_t - \sqrt{\alpha_t} x_0)^2 \right] \right\} \\ &= \exp \left\{ -\frac{1}{2} \left[ \frac{(x_t - \sqrt{\alpha_t} x_{t-1})^2}{1 - \alpha_t} + \frac{(x_{t-1} - \sqrt{\alpha_{t-1}} x_0)^2}{1 - \alpha_{t-1}} - \frac{(x_t - \sqrt{\alpha_t} x_0)^2}{1 - \alpha_t} \right] \right\} \\ &= \exp \left\{ -\frac{1}{2} \left[ \frac{2\sqrt{\alpha_t} x_t x_{t-1} + \alpha_t x_{t-1}^2}{1 - \alpha_t} + \frac{(x_{t-1}^2 - 2\sqrt{\alpha_{t-1}} x_{t-1} x_0)}{1 - \alpha_{t-1}} \right] + C(x_t, x_0) \right\} \\ &\propto \exp \left\{ -\frac{1}{2} \left[ \frac{2\sqrt{\alpha_t} x_t x_{t-1} + \alpha_t x_{t-1}^2}{1 - \alpha_t} + \frac{x_{t-1}^2}{1 - \alpha_{t-1}} - \frac{2\sqrt{\alpha_{t-1}} x_{t-1} x_0}{1 - \alpha_{t-1}} \right] \right\} \\ &= \exp \left\{ -\frac{1}{2} \left[ \frac{\alpha_t}{(1 - \alpha_t)} + \frac{1}{1 - \alpha_{t-1}} \right] x_{t-1}^2 - 2 \left( \frac{\sqrt{\alpha_t} x_t}{1 - \alpha_t} + \frac{\sqrt{\alpha_{t-1}} x_0}{1 - \alpha_{t-1}} \right) x_{t-1} \right\} \\ &= \exp \left\{ -\frac{1}{2} \left[ \frac{\alpha_t (1 - \alpha_{t-1}) + 1 - \alpha_t}{(1 - \alpha_t)(1 - \alpha_{t-1})} \right] x_{t-1}^2 - 2 \left( \frac{\sqrt{\alpha_t} x_t + \sqrt{\alpha_{t-1}} x_0}{1 - \alpha_t} \right) x_{t-1} \right\} \\ &= \exp \left\{ -\frac{1}{2} \left[ \frac{\alpha_t - \alpha_t \alpha_{t-1} + 1 - \alpha_t}{(1 - \alpha_t)(1 - \alpha_{t-1})} \right] x_{t-1}^2 - 2 \left( \frac{\sqrt{\alpha_t} x_t + \sqrt{\alpha_{t-1}} x_0}{1 - \alpha_t} \right) x_{t-1} \right\} \\ &= \exp \left\{ -\frac{1}{2} \left[ \frac{1 - \alpha_t}{(1 - \alpha_t)(1 - \alpha_{t-1})} \right] x_{t-1}^2 - 2 \left( \frac{\sqrt{\alpha_t} x_t + \sqrt{\alpha_{t-1}} x_0}{1 - \alpha_t} \right) x_{t-1} \right\} \\ &= \exp \left\{ -\frac{1}{2} \left[ \frac{1}{(1 - \alpha_t)(1 - \alpha_{t-1})} \right] x_{t-1}^2 - 2 \left( \frac{\sqrt{\alpha_t} x_t + \sqrt{\alpha_{t-1}} x_0}{(1 - \alpha_t)(1 - \alpha_{t-1})} \right) x_{t-1} \right\} \\ &= \exp \left\{ -\frac{1}{2} \left[ \frac{1}{(1 - \alpha_t)(1 - \alpha_{t-1})} \right] \left[ x_{t-1}^2 - 2 \frac{(\sqrt{\alpha_t} x_t + \sqrt{\alpha_{t-1}} x_0)(1 - \alpha_t)(1 - \alpha_{t-1})}{1 - \alpha_t} x_{t-1} \right] \right\} \\ &= \exp \left\{ -\frac{1}{2} \left[ \frac{1}{(1 - \alpha_t)(1 - \alpha_{t-1})} \right] \left[ x_{t-1}^2 - 2 \frac{\sqrt{\alpha_t}(1 - \alpha_{t-1}) x_t + \sqrt{\alpha_{t-1}}(1 - \alpha_t) x_0}{1 - \alpha_t} x_{t-1} \right] \right\} \\ &\propto \mathcal{N}(x_{t-1}; \frac{\sqrt{\alpha_t}(1 - \alpha_{t-1}) x_t + \sqrt{\alpha_{t-1}}(1 - \alpha_t) x_0}{1 - \alpha_t}, \frac{(1 - \alpha_t)(1 - \alpha_{t-1})}{2\alpha_t(t)}) \end{align*}$$

lemma 7

$$\begin{align*} &\arg\min_{\theta} D_{KL}(q(x_{t-1}|x_t, x_0) \parallel p_\theta(x_{t-1}|x_t)) \\ &= \arg\min_{\theta} D_{KL}(\mathcal{N}(x_{t-1}; \mu_q, \Sigma_q(t)) \parallel \mathcal{N}(x_{t-1}; \mu_\theta, \Sigma_q(t))) \\ &= \arg\min_{\theta} \frac{1}{2\sigma_q^2(t)} \left[ \left\| \frac{\sqrt{\alpha_t}(1 - \alpha_{t-1})x_t + \sqrt{\alpha_{t-1}}(1 - \alpha_t)\hat{x}_\theta(x_t, t)}{1 - \bar{\alpha}_t} - \frac{\sqrt{\alpha_t}(1 - \alpha_{t-1})x_t + \sqrt{\alpha_{t-1}}(1 - \alpha_t)x_0}{1 - \bar{\alpha}_t} \right\|_2^2 \right] \\ &= \arg\min_{\theta} \frac{1}{2\sigma_q^2(t)} \left[ \left\| \frac{\sqrt{\alpha_{t-1}}(1 - \alpha_t)\hat{x}_\theta(x_t, t)}{1 - \bar{\alpha}_t} - \frac{\sqrt{\alpha_{t-1}}(1 - \alpha_t)x_0}{1 - \bar{\alpha}_t} \right\|_2^2 \right] \\ &= \arg\min_{\theta} \frac{1}{2\sigma_q^2(t)} \left[ \left\| \frac{\sqrt{\alpha_{t-1}}(1 - \alpha_t)}{1 - \bar{\alpha}_t} (\hat{x}_\theta(x_t, t) - x_0) \right\|_2^2 \right] \\ &= \arg\min_{\theta} \frac{1}{2\sigma_q^2(t)} \frac{\alpha_{t-1}(1 - \alpha_t)^2}{(1 - \bar{\alpha}_t)^2} \left[ \left\| \hat{x}_\theta(x_t, t) - x_0 \right\|_2^2 \right] \\ &= \arg\min_{\theta} \frac{1}{2 \frac{(1 - \alpha_t)(1 - \bar{\alpha}_{t-1})}{1 - \bar{\alpha}_t}} \frac{\bar{\alpha}_{t-1}(1 - \alpha_t)^2}{(1 - \bar{\alpha}_t)^2} \left[ \left\| \hat{x}_\theta(x_t, t) - x_0 \right\|_2^2 \right] \\ &= \arg\min_{\theta} \frac{1}{2} \frac{1 - \bar{\alpha}_t}{(1 - \alpha_t)(1 - \bar{\alpha}_{t-1})} \frac{\bar{\alpha}_{t-1}(1 - \alpha_t)^2}{(1 - \bar{\alpha}_t)^2} \left[ \left\| \hat{x}_\theta(x_t, t) - x_0 \right\|_2^2 \right] \\ &= \arg\min_{\theta} \frac{1}{2} \frac{\bar{\alpha}_{t-1} - \bar{\alpha}_t}{(1 - \bar{\alpha}_{t-1})(1 - \bar{\alpha}_t)} \left[ \left\| \hat{x}_\theta(x_t, t) - x_0 \right\|_2^2 \right] \\ &= \arg\min_{\theta} \frac{1}{2} \frac{\bar{\alpha}_{t-1} - \bar{\alpha}_t - 1}{(1 - \bar{\alpha}_{t-1})(1 - \bar{\alpha}_t)} \left[ \left\| \hat{x}_\theta(x_t, t) - x_0 \right\|_2^2 \right] \\ &= \arg\min_{\theta} \frac{1}{2} \left( \frac{\bar{\alpha}_{t-1}(1 - \bar{\alpha}_t)}{1 - \bar{\alpha}_{t-1}(1 - \bar{\alpha}_t)} - \frac{\bar{\alpha}_t(1 - \bar{\alpha}_{t-1})}{(1 - \bar{\alpha}_{t-1})(1 - \bar{\alpha}_t)} \right) \left[ \left\| \hat{x}_\theta(x_t, t) - x_0 \right\|_2^2 \right] \\ &= \arg\min_{\theta} \frac{1}{2} \left( \frac{\bar{\alpha}_{t-1}}{1 - \bar{\alpha}_{t-1}} - \frac{\bar{\alpha}_t}{1 - \bar{\alpha}_t} \right) \left[ \left\| \hat{x}_\theta(x_t, t) - x_0 \right\|_2^2 \right] \end{align*}$$

lemma 8

$$\begin{align*} &\arg\min_{\theta} D_{KL}(q(x_{t-1}|x_t, x_0) \parallel p_\theta(x_{t-1}|x_t)) \\ &= \arg\min_{\theta} D_{KL}(\mathcal{N}(x_{t-1}; \mu_q, \Sigma_q(t)) \parallel \mathcal{N}(x_{t-1}; \mu_\theta, \Sigma_q(t))) \\ &= \arg\min_{\theta} \frac{1}{2\sigma_q^2(t)} \left[ \left\| \frac{1}{\sqrt{\alpha_t}} x_t - \frac{1 - \alpha_t}{\sqrt{1 - \bar{\alpha}_t}\sqrt{\alpha_t}} \hat{\epsilon}_\theta(x_t, t) - \frac{1}{\sqrt{\alpha_t}} x_t + \frac{1 - \alpha_t}{\sqrt{1 - \bar{\alpha}_t}\sqrt{\alpha_t}} \epsilon_0 \right\|_2^2 \right] \\ &= \arg\min_{\theta} \frac{1}{2\sigma_q^2(t)} \left[ \left\| \frac{1 - \alpha_t}{\sqrt{1 - \bar{\alpha}_t}\sqrt{\alpha_t}} \epsilon_0 - \frac{1 - \alpha_t}{\sqrt{1 - \bar{\alpha}_t}\sqrt{\alpha_t}} \hat{\epsilon}_\theta(x_t, t) \right\|_2^2 \right] \\ &= \arg\min_{\theta} \frac{1}{2\sigma_q^2(t)} \left[ \left\| \frac{1 - \alpha_t}{\sqrt{1 - \bar{\alpha}_t}\sqrt{\alpha_t}} (\epsilon_0 - \hat{\epsilon}_\theta(x_t, t)) \right\|_2^2 \right] \\ &= \arg\min_{\theta} \frac{1}{2\sigma_q^2(t)} \frac{(1 - \alpha_t)^2}{(1 - \bar{\alpha}_t)\alpha_t} \left[ \left\| \epsilon_0 - \hat{\epsilon}_\theta(x_t, t) \right\|_2^2 \right] \end{align*}$$